Particle Swarm Optimization: a parallelized approach
General Information
Parallel Particle Swarm Optimization (PSO) project delves into the realm of optimization techniques, focusing primarily on the concepts of “particles” and “particle perception.”
In the context of PSO, a particle is a fundamental entity characterized by:
- A position, denoted as $x$, representing a candidate solution for an optimization problem.
- A velocity component, denoted as $v$, which is used to perturb the particle’s position.
- A performance measure, denoted as $f(x)$ or fitness value, quantifying the quality of the candidate solution.
The entire collection of particles forms a “swarm.”
Each particle needs to perceive the positions and associated performance measures of neighboring particles. This allows each particle to remember the best performance position ($z$) among its neighbors and its own best performance ($y$) up to the current point.
This project implements a version of PSO employing a “distance-based” neighborhood approach in a nearest neighbor fashion. Specifically, each particle maintains a fixed number of neighbors, which dynamically adjusts based on the particle’s position within the landscape.
Parametrization
The PSO algorithm involves several critical parameters:
- Swarm size, typically around 20 particles for problems with a dimensionality ranging from 2 to 200.
- Neighborhood size, typically between 3 to 5 neighbors or a global neighborhood.
- Velocity update factors.
Continuous Optimization
The PSO begins with the initialization of a swarm of particles, each assigned random positions and velocities.
During each iteration, each particle updates its velocity using the equation:
$$v' = w \cdot v + \phi_1 U_1 \cdot (y - x) + \phi_2 U_2 \cdot (z - x)$$Here:
- $x$ and $v$ represent the particle’s current position and velocity.
- $y$ and $z$ denote the personal best and social/global best positions, respectively.
- $w$ stands for the inertia weight that factors in the current velocity.
- $\phi_1$ and $\phi_2$ are acceleration coefficients or learning rates, governing cognitive and social influences, respectively.
- $U_1$ and $U_2$ are random numbers uniformly distributed between 0 and 1.
Subsequently, each particle updates its position using:
$$x' = x + v'$$If there’s an improvement in performance, the particle updates its personal best ($y$) and potentially the global best ($z$).
State-of-the-Art Analysis
A review of existing PSO implementations revealed three primary categories:
- Algorithms that modify the PSO behavior by introducing new features.
- PSO implementations focused on solving specific real-world problems.
- Efforts aimed at optimizing the runtime execution speed.
The project excludes the second category as these solutions are highly problem-dependent. The first category is suitable for benchmarking analysis but often requires code modifications, leading to potential inconsistencies. The third category, which optimizes runtime speed, serves as the primary competitor, and various PSO versions have been implemented.
| Ref. | Year | Type | Code | Note |
|---|---|---|---|---|
| Kennedy, J. and Eberhart, R. | 1995 | Serial | No | - |
| toddguant | 2019 | Serial | Yes | 1 |
| sousouho | 2019 | Serial | Yes | 1 |
| kkentzo | 2020 | Serial | Yes | 1 |
| fisherling | 2020 | Serial | Yes | 1 |
| Antonio O.S. Moraes et al. | 2014 | MPI | No | - |
| Nadia Nedjah et al. | 2017 | MPI/MP | No | - |
| abhi4578 | 2019 | MPI/MP,CUDA | Yes | 1 |
| LaSEEB | 2020 | OpenMP | Yes | 2 |
| pg443 | 2021 | Serial,OpenMP | Yes | 1 |
The indexes in the notes refer to:
- provides only global neighborhood implementation. Thus, the comparison would be untruthful as those implementations have a clear advantage in the execution time due to a favorable topology;
- provides PSO with different neighborhood versions but without a distance based approach. Hence, the implication are the same as for the point 1.
Main Step Towards Parallelization
This project focused on achieving parallelization using a hybrid OpenMP-MPI approach. It introduced multiprocessing and efficient communication strategies to enhance PSO performance.
Serial Version of the Algorithm
The PSO algorithm’s core steps include particle initialization, position exchange among the swarm, particle sorting based on distance, and position and velocity updates. Initial attempts to parallelize with OpenMP revealed significant overhead for small problems, leading to slower execution times compared to the single-threaded model.
Parallel Version of the Algorithm
The workload was distributed among multiple processes using the MPI library, and multiprocessing was utilized through OpenMP for various shared-memory tasks.
Architecture
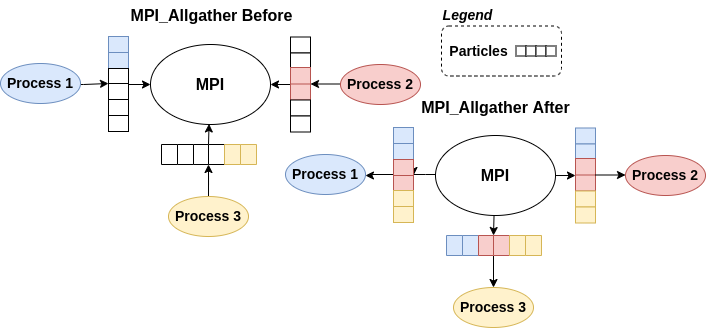
A parallel computational pattern, the “all-to-all” model, was implemented using MPI_Allgather to exchange individual messages among all processes.
Message
To facilitate inter-process communication, a custom MPI data type named “broadcastMessage_t” was introduced, containing information such as timestamps, iteration numbers, particle identifiers, sender ranks, and solution data.
Communication Pattern
Communication between processes was synchronous. Each process handled a portion of the particles, and particle information was exchanged using MPI_Allgather. The sorted particles enabled each process to identify the nearest neighbors for individual particles.
Benchmarking
A comprehensive benchmarking analysis was conducted by varying the number of threads, processes, and PBS process allocation patterns. The primary configuration included a problem dimension of 50, 5000 particles, 500 iterations, and other relevant parameters.
Results revealed that for thread parallelization, the overhead introduced by OpenMP often outweighed the performance benefits. Thread parallelization was found to be unsuitable for all problems due to the varying behavior of different systems.
Benchmarking mainly focused on the multi-process solution. Results showed that as the number of processes increased, the time required for communication also increased. The optimal scenario was observed when using a limited number of processes, as the overhead associated with MPI communication became significant with larger process counts.
Final Discussion
The project successfully developed a hybrid OpenMP-MPI algorithm for complex continuous optimization problems, equipped with a robust DevOps pipeline.
Thread parallelization was found to be ineffective for PSO, often leading to performance degradation due to excessive overhead. Benchmarking
Contributors
- Samuele Bortolotti
- Federico Izzo
