Unsupervised Domain Adaptation
General Information
Group project for the Deep Learning course of the Master’s Degree in Computer Science at University of Trento.
Description & Objectives
The main focus of this project is to build, train, and evaluate a deep learning framework on a standard setting of Unsupervised Domain Adaptation (UDA).
The test dataset on which the proposed methods are tested is the Adaptiope, a large scale, diverse UDA dataset with 3 domains: synthetic, product, and real-world data.
The implemented networks will be trained:
- in a supervised way on the source domain;
- in an unsupervised way on the target domain.
The gain, namely the amount of improvement we receive when we use the domain adaption framework compared to the outcome we get without any domain alignment approach, is used to assess the quality of the domain alignment strategy. The gain can be represented mathematically as:
$$ G = acc_{uda} - acc_{so} $$This has been be done in both directions between the two selected domains, using as evaluation metric the validation accuracy on the target domain:
$$ Accuracy = \frac{T_P + T_N}{T_P + T_N + F_P + F_N} $$Where:
- $TP$ stands for true positives, namely cases in which the algorithm correctly predicted the positive class.
- $TN$ stands for true negatives, namely cases in which the algorithm correctly predicted the negative class.
- $FP$ stands for false positives, namely cases in which samples are associated with the positive class whereas they belong to the negative one. (Also known as a “Type I error.”)
- $FN$ stands for false negatives, namely cases in which samples are associated with the negative class whereas they belong to the positive one. (Also known as a “Type II error.”)
Eventually lower and upper bounds will be calculated training the networks only on one specific domain (source domain for a lower bound, target domain for an upper bound), enabling us to provide some considerations about the achievements of our architectures.
Domain Adaptation
Just to give a formal background, we leverage on the definition of Domain Adaptation provided by Gabriela Csurka et.al which in the following sub-section will be presented.
We define a domain $D$ as a d-dimensional feature space $X \in \mathcal{R}^d$ based on a marginal probability distribution $P(X)$, and a task $T$ is defined as a conditional probability distribution $P(Y|X)$ where $Y$ is the label space. Given sample set $X = \{x_1, \cdots x_n\}$ of $X$ and their corresponding labels $Y = \{y_1, \cdots y_n\}$ from $Y$. In general, these feature-label pairings $\{x_i, y_i\}$ may be used in order to learn the probability distribution $P(Y|X)$ in a supervised way. Let us assume we have two domains with their related tasks: a source domain $D_s = {X_s, P(X_s)}$ with $T_s = {Y_s, P(Y_s|X_s)}$ and a target domain $Dt = {X_t, P(X_t)}$ with $T_t = {Y_t, P(Y_t|X_t)}$. If the two domains corresponds, namely $D_s = D_t$ and $T_s = T_t$, traditional machine learning methods can be used to solve the problem, where $D_s$ becomes the training set and $D_t$ the test set. However, this assumption is violated, $D_t \neq D_s$ or $T_t \neq T_s$, the models trained on $D_s$ might perform poorly on $D_t$, or they are not applicable directly if $T_t \neq T_s$. Futhermore, when the source domain is related to the target, it is possible to exploit the related information from $\{D_s, T_s\}$ to learn $P(Y_t|X_t)$.This process is known as transfer learning.
Domain Adaptation typically refers to situations in which the tasks remain the same ($T_t = T_s$), but the domains differ ($D_s \neq D_t$). In classification tasks, it is assumed that both the set of labels and the conditional distributions are shared between the two domains, i.e., $Y_s = Y_t$ and $P(Y|X_t) = P(Y|X_s)$. However, the second assumption, $P(Y|X_t) = P(Y|X_s)$, is quite strong and may not always hold in real-world scenarios. Consequently, the definition of domain adaptation is often simplified to only require the first assumption, namely $Y_s = Y_t = Y$.Furthermore, the Domain Adaptation field distinguishes between two scenarios:
- Unsupervised Domain Adaptation, where labels are only available for the source domain.
- Semi-supervised Domain Adaptation, where only a limited number of target samples are labeled.
Proposed Solutions
When addressing Deep Domain Adaptation problems, there are three primary approaches:
- Discrepancy-based methods: These methods align the domain data representation using statistical measures.
- Adversarial-based methods: They involve a domain discriminator to enforce domain confusion.
- Reconstruction-based methods: These methods use an auxiliary reconstruction task to ensure a domain-invariant feature representation.
This repository includes solutions for each of these methods, as well as a custom solution that combines two of them: discrepancy-based and reconstruction-based (DSN + MEDM).
Due to the limited availability of examples, training a network from scratch has not yielded satisfactory results. Therefore, we start with a feature extractor pre-trained on the ImageNet object recognition dataset.
Additionally, to explore the proposed methods thoroughly, we provide the option to evaluate the domain adaptation method using two different backbone networks: AlexNet and ResNet18.
Network Architectures
To effectively address the domain adaptation challenge, we have implemented various network architectures adapted from relevant research papers and tailored to our requirements.
Our primary objective, as stated in the introduction, is to assess the performance (gain) of some of the most significant approaches in the domain adaptation field, integrated with two of the most prominent convolutional neural network architectures: AlexNet and ResNet.
In this repository, we cover:
- Deep Domain Confusion Networks
- Domain Adversarial Neural Network
- Domain Separation Networks
- Rotation loss Network
- Entropy Minimization vs. Diversity Maximization for Domain Adaptation
- Our attempt to combine
MEDMwithDANN - Another approach to combine
MEDMwithDSN
Results
In this project, we explored various architecture categories for domain adaptation techniques, including discrepancy-based, adversarial-based, and reconstruction-based. Notably, the most effective approaches were DANN and MEDM.
MEDM is a versatile approach that can be seamlessly integrated into any architecture, featuring two straightforward entropy losses that result in stable training and impressive performance. In contrast, DANN is more susceptible to hyperparameter variations and often leads to unstable training.
During our experiments, we found that combining DSN and MEDM proved effective, while combining MEDM and DANN did not consistently yield improvement.
Adapting from the product domain to the real world is more challenging, but it offers a greater potential for improvement since there is more room between the baseline and the upper bound. Conversely, transitioning between real-world and product images ensures higher accuracy because the networks have been pretrained on ImageNet. Consequently, the gap between the baseline and the real world is narrower, making significant progress more challenging.
After testing both AlexNet and ResNet18 as backbone architectures, we discovered that not only did ResNet18 exhibit higher baseline and upper-bound values, but all domain adaptation strategies also generated substantially greater gains.
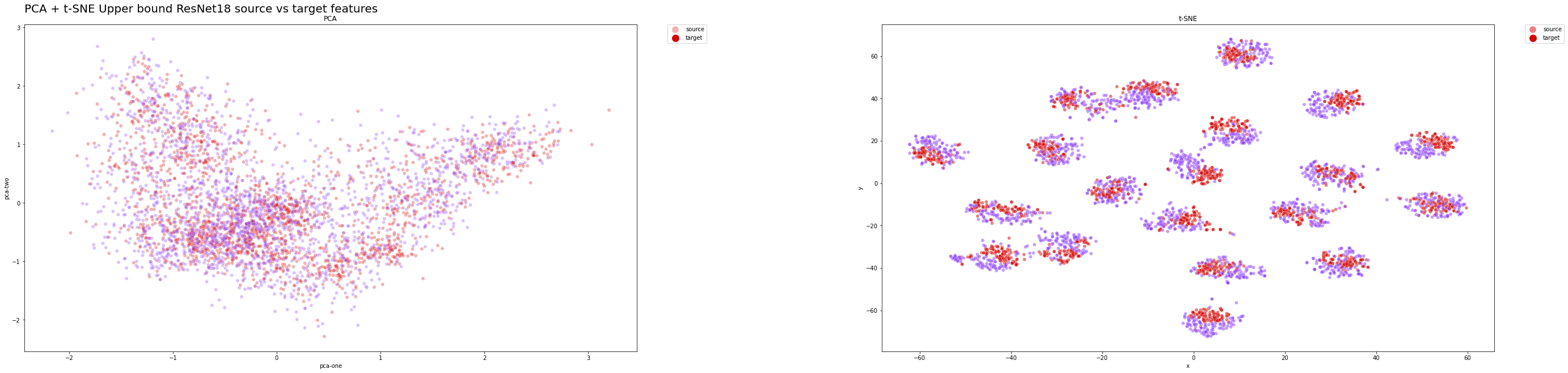
t-SNE plots clearly demonstrated that our final solution effectively extracts relevant features from both domains while maintaining accurate classification. The distributions closely resemble the optimal ones, represented by the upper bound ResNet18 model.
Distribution Alignment Plots
We have included plots that illustrate how features from the target and source domains are distributed using dimensionality reduction techniques.
For instance, we present the product-to-real-world domain adaptation, focusing on the best-performing model, namely DSN + MEDM. To provide an effective representation of distribution alignment and consolidate the most significant graph for our project, we present two graphs:
- The distribution of features learned by the backbone neural network (ResNet18 in both cases), excluding the classifier or bottleneck layers.
- The predicted class distribution.
Note: Both plots are generated based on the target domain (
real-world), which theDSN+MEDMapproach does not have access to.
Ideally, we aim for our domain adaptation model to achieve performance similar to that of the upper-bound model, which provides the best generalization for both source and target domain samples. Therefore, the model’s feature distribution is a valuable metric for assessing the quality of the domain adaptation technique.
Upper Bound Features Distribution on the Test Set:
Upper Bound Classes Distribution on the Test Set:

We expect both the classes and features distribution to align closely with the target distributions, as the model has achieved remarkable performance.
DSN + MEDM Features Distribution on the Test Set:
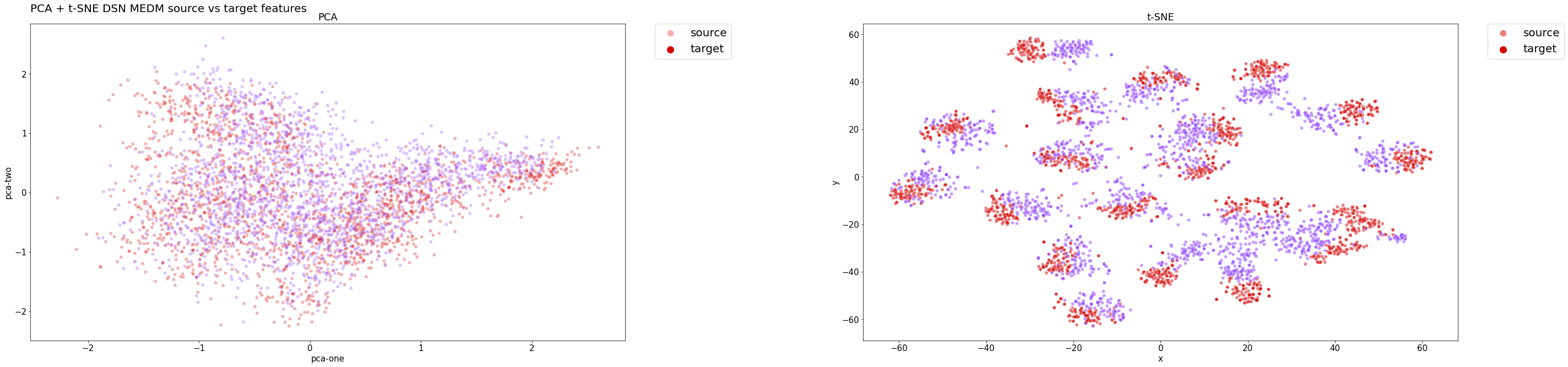
As evidenced by the class distributions below, the model’s classifier effectively clusters examples while maintaining high accuracy. Clusters are well-defined and separated, even for target domain examples, which are correctly classified.
DSN + MEDM Classes Distribution on the Test Set:

In both cases, PCA did not provide significant insights into the results, as a linear transformation may be too simplistic for reducing high-dimensional data to a lower-dimensional embedding.
Performance
Here are the results we achieved on the smaller version of Adaptiope:
| Backbone Network | Method | Source set | Target set | Accuracy on target (\%) | Gain |
|---|---|---|---|---|---|
| AlexNet | Source Only | Product Images | Real Life | 64.45 | 0 |
| ResNet18 | Source Only | Product Images | Real Life | 75.39 | 0 |
| AlexNet | Upper Bound | Product Images | Real Life | 85.94 | 21.485 |
| ResNet18 | Upper Bound | Product Images | Real Life | 96.88 | 20.312 |
| AlexNet | DDC | Product Images | Real Life | 68.36 | 3.91 |
| ResNet18 | DDC | Product Images | Real Life | 83.50 | 8.11 |
| AlexNet | DANN | Product Images | Real Life | 65.23 | 0.78 |
| ResNet18 | DANN | Product Images | Real Life | 87.11 | 11.72 |
| OriginalDSN | Product Images | Real Life | 04.17 | ||
| AlexNet | BackboneDSN | Product Images | Real Life | 58.85 | -5.60 |
| ResNet18 | BackboneDSN | Product Images | Real Life | 78.39 | 3.00 |
| ResNet18 | OptimizedDSN | Product Images | Real Life | 81.25 | 5.86 |
| ResNet18 | Rotation Loss | Product Images | Real Life | 73.83 | -1.56 |
| ResNet18 | MEDM | Product Images | Real Life | 90.36 | 14.97 |
| ResNet18 | MEDM + DANN | Product Images | Real Life | 80.21 | 4.82 |
| ResNet18 | MEDM + DSN | Product Images | Real Life | 91.15 | 15.76 |
| AlexNet | Source Only | Real Life | Product Images | 85.55 | 0 |
| ResNet18 | Source Only | Real Life | Product Images | 93.75 | 0 |
| AlexNet | Upper Bound | Real Life | Product Images | 95.70 | 10.15 |
| ResNet18 | Upper Bound | Real Life | Product Images | 98.05 | 4.3 |
| AlexNet | DDC | Real Life | Product Images | 82.03 | -3.52 |
| ResNet18 | DDC | Real Life | Product Images | 94.53 | 0.78 |
| AlexNet | DANN | Real Life | Product Images | 83.98 | -1.57 |
| ResNet18 | DANN | Real Life | Product Images | 96.09 | 2.34 |
| OriginalDSN | Real Life | Product Images | 04.17 | ||
| AlexNet | BackboneDSN | Real Life | Product Images | 84.11 | -1.44 |
| ResNet18 | BackboneDSN | Real Life | Product Images | 91.41 | -2.34 |
| ResNet18 | OptimizedDSN | Real Life | Product Images | 93.49 | -0.26 |
| ResNet18 | Rotation Loss | Real Life | Product Images | 91.80 | -1.95 |
| ResNet18 | MEDM | Real Life | Product Images | 97.14 | 3.39 |
| ResNet18 | MEDM + DANN | Real Life | Product Images | 94.00 | 0.25 |
| ResNet18 | MEDM + DSN | Real Life | Product Images | 96.61 | 2.86 |
Contributors
- Samuele Bortolotti
- Luca De Menego
