Unsupervised Domain Adaptation
Allgemeine Informationen
Gruppenprojekt für den Kurs Deep Learning des Masterstudiengangs Informatik an der Universität Trient.
Beschreibung & Zielsetzung
Das Hauptaugenmerk dieses Projekts liegt auf der Entwicklung, dem Training und der Evaluierung eines Deep-Learning-Frameworks auf einem Standarddatensatz von [Unsupervised Domain Adaptation (UDA)] (https://en.wikipedia.org/wiki/Domain_adaptation).
Der Testdatensatz, auf dem die vorgeschlagenen Methoden getestet werden, ist der Adaptiope, ein groß angelegter, vielfältiger UDA-Datensatz mit 3 Domänen: synthetische, Produkt- und reale Daten.
Die implementierten Netzwerke werden trainiert:
- auf überwachte Weise in der Quelldomäne;
- auf unbeaufsichtigte Weise auf der Zieldomäne.
Der Gewinn, d. h. die Höhe der Verbesserung, die wir bei Verwendung des Rahmens für die Domänenanpassung im Vergleich zu dem Ergebnis erhalten, das wir ohne jeglichen Ansatz für die Domänenanpassung erhalten, wird zur Bewertung der Qualität der Strategie für die Domänenanpassung verwendet. Der Gewinn kann mathematisch wie folgt dargestellt werden:
$$ G = acc_{uda} - acc_{so} $$Dies wurde in beiden Richtungen zwischen den beiden ausgewählten Domänen durchgeführt, wobei als Bewertungsmaßstab die Validierungsgenauigkeit auf der Zieldomäne verwendet wurde:
$$ Genauigkeit = \frac{T_P + T_N}{T_P + T_N + F_P + F_N} $$Wobei:
- $TP$ steht für echte Positive, d. h. Fälle, in denen der Algorithmus die positive Klasse korrekt vorhergesagt hat.
- $TN$ steht für echte Negative, d.h. Fälle, in denen der Algorithmus die negative Klasse richtig vorhergesagt hat.
- $FP$ steht für falsch positive Ergebnisse, d. h. Fälle, in denen Proben der positiven Klasse zugeordnet werden, obwohl sie zur negativen Klasse gehören. (Auch bekannt als “Fehler vom Typ I”.)
- $FN$ steht für falsch negativ, d. h. für Fälle, in denen Proben der negativen Klasse zugeordnet werden, obwohl sie der positiven Klasse angehören. (Auch bekannt als “Fehler vom Typ II”.)
Schließlich werden untere und obere Schranken berechnet, indem die Netze nur auf einer bestimmten Domäne trainiert werden (Quelldomäne für eine untere Schranke, Zieldomäne für eine obere Schranke), so dass wir einige Überlegungen zu den Leistungen unserer Architekturen anstellen können.
Domänenanpassung
Um einen formalen Hintergrund zu schaffen, stützen wir uns auf die Definition von Domain Adaptation von [Gabriela Csurka et.al] (https://arxiv.org/pdf/1702.05374.pdf), die im folgenden Unterabschnitt vorgestellt wird.
Wir definieren eine Domäne $D$ als einen d-dimensionalen Merkmalsraum $X \in \mathcal{R}^d$ basierend auf einer marginalen Wahrscheinlichkeitsverteilung $P(X)$, und eine Aufgabe $T$ ist definiert als eine bedingte Wahrscheinlichkeitsverteilung $P(Y|X)$, wobei $Y$ der Labelraum ist. Gegeben ist eine Stichprobenmenge $X = \{x_1, \cdots x_n\}$ von $X$ und ihre entsprechenden Labels $Y = \{y_1, \cdots y_n\}$ aus $Y$. Im Allgemeinen können diese Merkmal-Label-Paare $\{x_i, y_i\}$ verwendet werden, um die Wahrscheinlichkeitsverteilung $P(Y|X)$ auf überwachte Weise zu lernen. Nehmen wir an, wir haben zwei Domänen mit ihren zugehörigen Aufgaben: eine Quelldomäne $D_s = {X_s, P(X_s)}$ mit $T_s = {Y_s, P(Y_s|X_s)}$ und eine Zieldomäne $Dt = {X_t, P(X_t)}$ mit $T_t = {Y_t, P(Y_t|X_t)}$. Wenn die beiden Domänen übereinstimmen, nämlich $D_s = D_t$ und $T_s = T_t$, können zur Lösung des Problems traditionelle Methoden des maschinellen Lernens verwendet werden, wobei $D_s$ die Trainingsmenge und $D_t$ die Testmenge wird. Wird diese Annahme jedoch verletzt, $D_t \neq D_s$ oder $T_t \neq T_s$, können die auf $D_s$ trainierten Modelle auf $D_t$ schlecht abschneiden, oder sie sind nicht direkt anwendbar, wenn $T_t \neq T_s$. Wenn die Quelldomäne mit der Zieldomäne verwandt ist, ist es außerdem möglich, die verwandten Informationen aus $\{D_s, T_s\}$ zu nutzen, um $P(Y_t|X_t)$ zu lernen.Dieser Prozess wird als Transferlernen bezeichnet.
Domänenanpassung bezieht sich typischerweise auf Situationen, in denen die Aufgaben gleich bleiben ($T_t = T_s$), aber die Domänen sich unterscheiden ($D_s \neq D_t$). Bei Klassifizierungsaufgaben wird davon ausgegangen, dass sowohl die Menge der Beschriftungen als auch die bedingten Verteilungen in den beiden Domänen gleich sind, d. h. $Y_s = Y_t$ und $P(Y|X_t) = P(Y|X_s)$. Die zweite Annahme, $P(Y|X_t) = P(Y|X_s)$, ist jedoch recht streng und trifft in der Praxis nicht immer zu. Daher wird die Definition der Domänenanpassung oft so vereinfacht, dass nur die erste Annahme erforderlich ist, nämlich $Y_s = Y_t = Y$.Außerdem wird im Bereich der Domänenanpassung zwischen zwei Szenarien unterschieden:
- Unüberwachte Domänenanpassung, bei der Beschriftungen nur für die Quelldomäne verfügbar sind.
- Halbüberwachte Bereichsanpassung, bei der nur eine begrenzte Anzahl von Zielproben beschriftet ist.
Vorgeschlagene Lösungen
Bei der Lösung von Problemen der Deep Domain Adaptation gibt es drei Hauptansätze:
- Diskrepanzbasierte Methoden: Diese Methoden gleichen die Darstellung der Domänendaten mit Hilfe statistischer Maße ab.
- Adversarial-basierte Methoden: Sie beinhalten einen Domänendiskriminator, um Domänenkonfusion zu erzwingen.
- Rekonstruktionsbasierte Methoden: Diese Methoden verwenden eine zusätzliche Rekonstruktionsaufgabe, um eine domäneninvariante Merkmalsdarstellung zu gewährleisten.
Dieses Repository enthält Lösungen für jede dieser Methoden sowie eine benutzerdefinierte Lösung, die zwei von ihnen kombiniert: diskrepanzbasierte und rekonstruktionsbasierte (DSN + MEDM).
Aufgrund der begrenzten Verfügbarkeit von Beispielen hat das Training eines Netzwerks von Grund auf keine zufriedenstellenden Ergebnisse geliefert. Daher beginnen wir mit einem Merkmalsextraktor, der auf dem ImageNet Objekterkennungsdatensatz trainiert wurde.
Um die vorgeschlagenen Methoden gründlich zu untersuchen, bieten wir außerdem die Möglichkeit, die Domänenanpassungsmethode mit zwei verschiedenen Backbone-Netzwerken zu evaluieren: AlexNet und ResNet18.
Netzwerk-Architekturen
Um die Herausforderung der Domänenanpassung effektiv zu bewältigen, haben wir verschiedene Netzwerkarchitekturen implementiert, die aus einschlägigen Forschungsarbeiten übernommen und auf unsere Anforderungen zugeschnitten wurden.
Unser primäres Ziel ist es, wie in der Einleitung erwähnt, die Leistung (Gewinn) einiger der wichtigsten Ansätze im Bereich der Domänenanpassung zu bewerten, die in zwei der bekanntesten Architekturen für faltbare neuronale Netze integriert sind: AlexNet” und “ResNet”.
In diesem Repository decken wir ab:
- Deep Domain Confusion Networks
- Domain Adversarial Neural Network
- Domain Separation Networks
- Rotation loss Network
- Entropy Minimization vs. Diversity Maximization for Domain Adaptation
- Unser Versuch,
MEDMmitDANNzu kombinieren - Ein anderer Ansatz,
MEDMmitDSNzu kombinieren
Ergebnisse
In diesem Projekt haben wir verschiedene Architekturkategorien für Domänenanpassungstechniken erforscht, darunter Diskrepanz-basiert, Adversarial-basiert und Rekonstruktions-basiert. Die effektivsten Ansätze waren DANN und MEDM.
MEDM” ist ein vielseitiger Ansatz, der sich nahtlos in jede Architektur integrieren lässt und sich durch zwei einfache Entropieverluste auszeichnet, die zu stabilem Training und beeindruckender Leistung führen. Im Gegensatz dazu ist DANN anfälliger für Hyperparameter-Variationen und führt oft zu instabilem Training.
Bei unseren Experimenten haben wir festgestellt, dass die Kombination von DSN und MEDM sich als effektiv erwiesen hat, während die Kombination von MEDM und DANN keine konsistente Verbesserung brachte.
Die Anpassung von der Produktdomäne an die reale Welt ist schwieriger, bietet aber ein größeres Verbesserungspotenzial, da mehr Spielraum zwischen der Basislinie und der oberen Grenze besteht. Umgekehrt gewährleistet der Übergang von der realen Welt zu Produktbildern eine höhere Genauigkeit, da die Netze zuvor auf “ImageNet” trainiert worden sind. Folglich ist die Lücke zwischen der Basislinie und der realen Welt kleiner, was signifikante Fortschritte schwieriger macht.
Nachdem wir sowohl AlexNet als auch ResNet18 als Backbone-Architekturen getestet hatten, stellten wir fest, dass ResNet18 nicht nur höhere Werte für die Basislinie und die obere Grenze aufwies, sondern dass alle Domänenanpassungsstrategien auch wesentlich größere Gewinne erzielten.
Die t-SNE-Diagramme zeigen deutlich, dass unsere endgültige Lösung effektiv relevante Merkmale aus beiden Domänen extrahiert und gleichzeitig eine genaue Klassifizierung gewährleistet. Die Verteilungen ähneln sehr stark den optimalen Verteilungen, die durch das Modell “ResNet18” mit der oberen Grenze dargestellt werden.
Plots der Verteilungsanpassung
Wir haben Diagramme eingefügt, die veranschaulichen, wie die Merkmale der Ziel- und Quelldomäne mithilfe von Dimensionalitätsreduktionstechniken verteilt werden.
Wir stellen zum Beispiel die “Produkt-zu-Realwelt”-Domänenanpassung dar und konzentrieren uns dabei auf das leistungsstärkste Modell, nämlich “DSN” + “MEDM”. Um eine effektive Darstellung der Verteilungsanpassung zu ermöglichen und den wichtigsten Graphen für unser Projekt zu konsolidieren, stellen wir zwei Graphen vor:
- Die Verteilung der Merkmale, die vom neuronalen Backbone-Netz (in beiden Fällen ResNet18) gelernt wurden, ohne die Klassifizierungs- oder Engpass-Schichten.
- Die vorhergesagte Klassenverteilung.
Anmerkung: Beide Diagramme werden auf der Grundlage der Zieldomäne (reale Welt) erstellt, zu der der Ansatz “DSN+MEDM” keinen Zugang hat.
Im Idealfall soll unser Domänenanpassungsmodell eine ähnliche Leistung erzielen wie das Modell der oberen Grenze, das die beste Verallgemeinerung sowohl für die Quell- als auch für die Zieldomäne bietet. Daher ist die Merkmalsverteilung des Modells ein wertvoller Maßstab für die Bewertung der Qualität der Domänenanpassungstechnik.
Verteilung der Merkmale der oberen Schranke im Testsatz:
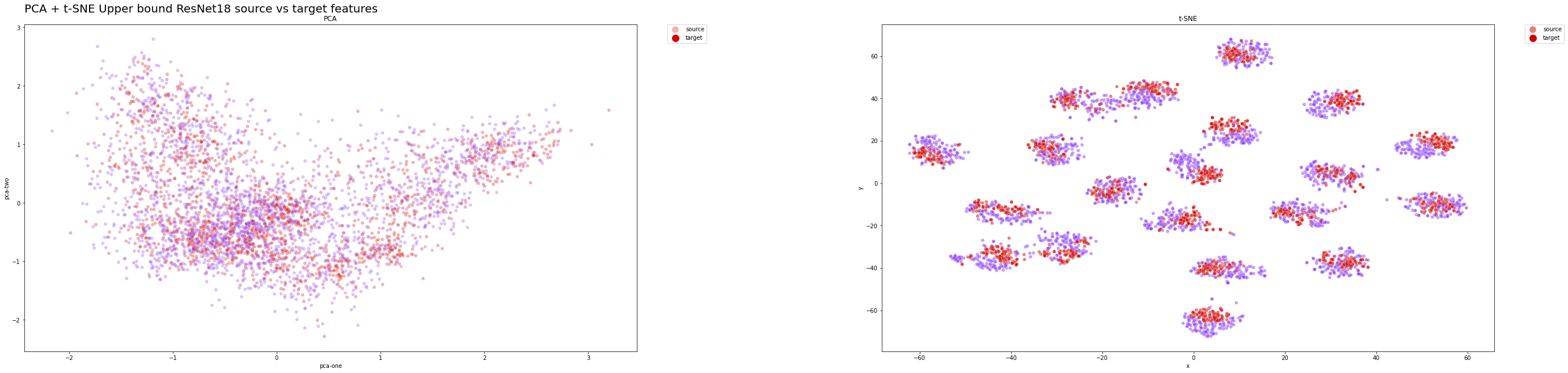
Obergrenzen-Klassenverteilung auf der Testmenge:

Wir erwarten, dass sowohl die Klassen- als auch die Merkmalsverteilung eng mit den Zielverteilungen übereinstimmen, da das Modell eine bemerkenswerte Leistung erzielt hat.
DSN + MEDM Features Verteilung auf dem Testset:
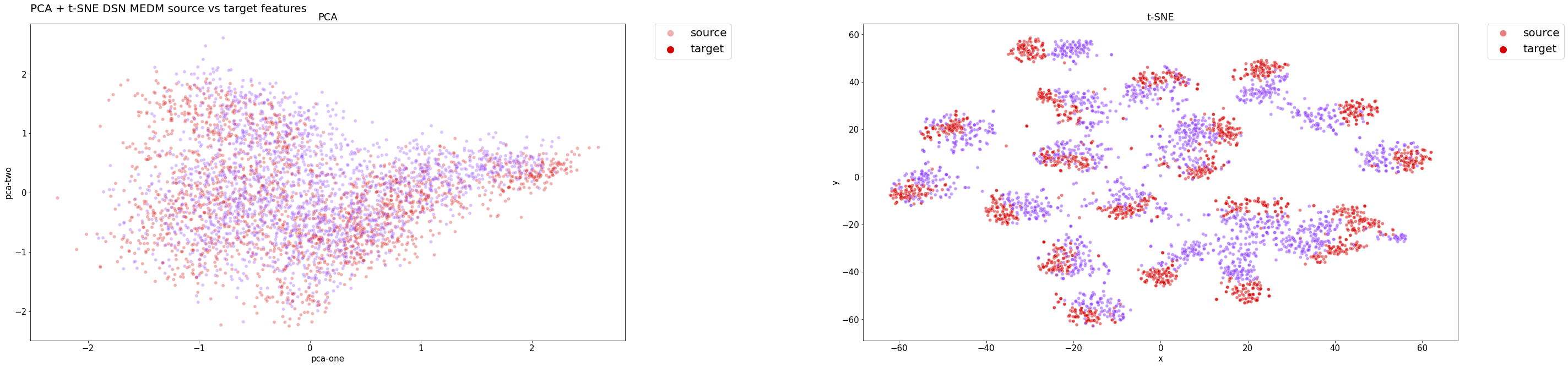
Wie die nachstehenden Klassenverteilungen zeigen, clustert der Klassifikator des Modells die Beispiele effektiv und behält dabei eine hohe Genauigkeit bei. Die Cluster sind gut definiert und voneinander getrennt, auch für die Beispiele aus dem Zielbereich, die korrekt klassifiziert werden.
DSN + MEDM-Klassenverteilung auf der Testmenge:

In beiden Fällen lieferte die PCA keine signifikanten Einblicke in die Ergebnisse, da eine lineare Transformation möglicherweise zu einfach ist, um hochdimensionale Daten auf eine niedriger dimensionale Einbettung zu reduzieren.
Leistung
Hier sind die Ergebnisse, die wir mit der kleineren Version von Adaptiope erzielt haben:
| Backbone-Netzwerk | Methode | Quellmenge | Zielmenge | Genauigkeit beim Ziel (\%) | Gewinn |
|---|---|---|---|---|---|
| AlexNet | Nur Quelle | Produktbilder | Realistisches Leben | 64,45 | 0 |
| ResNet18 | Nur Quelle | Produktbilder | Realistisches Leben | 75,39 | 0 |
| AlexNet | Obergrenze | Produktbilder | Realistisches Leben | 85,94 | 21,485 |
| ResNet18 | Obergrenze | Produktbilder | Realistisches Leben | 96,88 | 20,312 |
| AlexNet | DDC | Produktbilder | Realistisches Leben | 68,36 | 3,91 |
| ResNet18 | DDC | Produktbilder | Realistisches Leben | 83,50 | 8,11 |
| AlexNet | DANN | Produktbilder | Realistisches Leben | 65,23 | 0,78 |
| ResNet18 | DANN | Produktbilder | Realistisches Leben | 87,11 | 11,72 |
| OriginalDSN | Produktbilder | Realistisches Leben | 04,17 | ||
| AlexNet | BackboneDSN | Produktbilder | Realistisches Leben | 58,85 | -5,60 |
| ResNet18 | BackboneDSN | Produktbilder | Realistisches Leben | 78,39 | 3,00 |
| ResNet18 | OptimizedDSN | Produktbilder | Realistisches Leben | 81,25 | 5,86 |
| ResNet18 | Rotation Loss | Produktbilder | Realistisches Leben | 73,83 | -1,56 |
| ResNet18 | MEDM | Produktbilder | Realistisches Leben | 90,36 | 14,97 |
| ResNet18 | MEDM + DANN | Produktbilder | Realistisches Leben | 80,21 | 4,82 |
| ResNet18 | MEDM + DSN | Produktbilder | Realistisches Leben | 91,15 | 15,76 |
| AlexNet | Nur Quelle | Realistisches Leben | Produktbilder | 85,55 | 0 |
| ResNet18 | Nur Quelle | Realistisches Leben | Produktbilder | 93,75 | 0 |
| AlexNet | Obergrenze | Realistisches Leben | Produktbilder | 95,70 | 10,15 |
| ResNet18 | Obergrenze | Realistisches Leben | Produktbilder | 98,05 | 4,3 |
| AlexNet | DDC | Realistisches Leben | Produktbilder | 82,03 | -3,52 |
| ResNet18 | DDC | Realistisches Leben | Produktbilder | 94,53 | 0,78 |
| AlexNet | DANN | Realistisches Leben | Produktbilder | 83,98 | -1,57 |
| ResNet18 | DANN | Realistisches Leben | Produktbilder | 96,09 | 2,34 |
| OriginalDSN | Realistisches Leben | Produktbilder | 04,17 | ||
| AlexNet | BackboneDSN | Realistisches Leben | Produktbilder | 84,11 | -1,44 |
| ResNet18 | BackboneDSN | Realistisches Leben | Produktbilder | 91,41 | -2,34 |
| ResNet18 | DSN Ottimizzata | Realistisches Leben | Produktbilder | 93,49 | -0,26 |
| ResNet18 | Rotation Loss | Realistisches Leben | Produktbilder | 91,80 | -1,95 |
| ResNet18 | MEDM | Realistisches Leben | Produktbilder | 97,14 | 3,39 |
| ResNet18 | MEDM + DANN | Realistisches Leben | Produktbilder | 94,00 | 0,25 |
| ResNet18 | MEDM + DSN | Realistisches Leben | Produktbilder | 96,61 | 2,86 |
Mitwirkende
- Samuele Bortolotti
- Luca De Menego
